离散数学II概览

集合论

集合

集合与元素

• 列举法
• 部分列举法
• 抽象法：谓词$P(x)$要明确清楚；不能取$P(x):x \notin x$这样的谓词定义集合。
• 归纳定义法

集合间的相等和包含关系

略。

幂集

集合A的全部子集构成的集合称为A的幂集，记作$\mathcal{P}(A) = \{ X \mid X \subseteq A \}$

有穷集的幂集的基数：有穷集合A重所含有元素的个数成为A的技术，记作$\#A$

• 若集合$S$是有穷集合，则$\mathcal{P}(S)$也是有穷集合，反之亦然。

定理：设$A$是有穷集合，则$\#\mathcal{P}(a)=2^{\#A}$

集合的运算

交集，并集，差集，补集，对称差

定理：

i) $A \subseteq A \cup B$ 且 $B \subseteq A \cup B$;
ii) $A \cap B \subseteq A$ 且 $A \cap B \subseteq B$;
iii) $A - B \subseteq A$;
iv) $A - B = A \cap {\sim}B$;
v) 若 $A \subseteq B$, 则 ${\sim}B \subseteq {\sim}A$;
vi) 若 $A \subseteq C$ 且 $B \subseteq C$, 则 $A \cup B \subseteq C$;
vii) 若 $A \subseteq B$ 且 $A \subseteq C$, 则 $A \subseteq B \cap C$。

幂等律，交换律，结合律，分配律，同一律，零律，否定律，吸收律，德摩根律，对合律

对偶原理：在不含-的集合恒等式中，将$\cup$和$\cap$呼唤，$\emptyset$和$U$互换，得到的仍是集合恒等式

定理：设$A$和$B$是全集$U$的子集，$B=~A$当且仅当$A\cup B=U$和$A\cap B=\varnothing$

定理：设$A$和$B$是全集$U$的子集，则下列命题等价：(1) $A \subseteq B$; (2) $A \cup B = B$; (3) $A \cap B = A$; (4) $A - B = \varnothing$

广义交，广义并

如果一个集合的所有元素都是集合，则称该集合为集类

定理：

(1) 若 $\mathcal{B} \neq \varnothing$, 则 $A \cup (\bigcup \mathcal{B}) = \bigcup \{ A \cup B \mid B \in \mathcal{B} \}$
(2) 若 $\mathcal{B} \neq \varnothing$, 则 $A \cap (\bigcap \mathcal{B}) = \bigcap \{ A \cap B \mid B \in \mathcal{B} \}$
(3) 若 $\mathcal{B} \neq \varnothing$, 则 $A \cup (\bigcap \mathcal{B}) = \bigcap \{ A \cup B \mid B \in \mathcal{B} \}$
(4) $A \cap (\bigcup \mathcal{B}) = \bigcup \{ A \cap B \mid B \in \mathcal{B} \}$
(5) 若 $\mathcal{B} \neq \varnothing$, 则 ${\sim}(\bigcap \mathcal{B}) = \bigcup \{ {\sim}B \mid B \in \mathcal{B} \}$
(6) 若 $\mathcal{B} \neq \varnothing$, 则 ${\sim}(\bigcup \mathcal{B}) = \bigcap \{ {\sim}B \mid B \in \mathcal{B} \}$

定理：设$A$为任意集合，$\mathcal{B}$为任意集类。

(1) 若 $B \in \mathcal{B}$, 则 $\bigcap \mathcal{B} \subseteq B$ 且 $B \subseteq \bigcup \mathcal{B}$;
(2) 若对每个 $B \in \mathcal{B}$ 皆有 $A \subseteq B$, 则 $A \subseteq \bigcap \mathcal{B}$ ($\mathcal{B} \neq \varnothing$ 时);
(3) 若对每个 $B \in \mathcal{B}$ 皆有 $B \subseteq A$, 则 $\bigcup \mathcal{B} \subseteq A$.

定理：设$\mathcal{A}，\mathcal{B}$为任意集类，则有

$\bigcup (\mathcal{A} \cup \mathcal{B}) = \bigcup \{ A \cup B \mid A \in \mathcal{A} \text{ 且 } B \in \mathcal{B} \}= (\bigcup \mathcal{A}) \cup (\bigcup \mathcal{B})$

有穷集的计数原理

略。

集合的归纳定义法

1. 基本项：非空集$S_{0}\subseteq A$（规定$A$的一些生成元）
2. 归纳项
3. 极小化（保证A是同时满足12的最小集合）
   • $A$中每个元素都通过有限次1或2获得
   • 如果集合$S$也满足1，2，则$A\subseteq S$
   • 如果集合$S\subseteq A$也满足1，2，则$S=A$

有序偶和笛卡尔乘积

有序偶的集合定义：$<x,y>={ { x } , { x,y } }$

定理：有序偶的唯一性定理：$<u,v>=<x,y>$当且仅当$u=x$和$v=y$

n元序偶$<x_1,x_2,...,x_n>$称$x_i$为第$i$个分量

定理：二元有序偶定理的推广。

笛卡尔乘积

定理：设$A,B$为任意两个集合，则$A×B=\varnothing$当且仅当$A=\varnothing$或$B=\varnothing$

定理：若$A,B$为任意两个有限集，则$\#(A×B)=\#A·\#B$

定理:设$A,B,C,D$为任意四个非空集合，则
(1)$A×B\subseteq C×D$当且仅当$A\subseteq C$且$B\subseteq D$
(2)$A×B=C×D$当且仅当$A=C$且$B=D$

定理：

(1) $A \times (B \cup C) = (A \times B) \cup (A \times C)$;
(2) $(A \cup B) \times C = (A \times C) \cup (B \times C)$;
(3) $A \times (B \cap C) = (A \times B) \cap (A \times C)$;
(4) $(A \cap B) \times C = (A \times C) \cap (B \times C)$;
(5) $A \times (B - C) = (A \times B) - (A \times C)$;
(6) $(A - B) \times C = (A \times C) - (B \times C)$。

可把两个集合的笛卡尔积推广到多个集合上。

关系

n元关系，二元关系，空关系，全关系

全域关系：$U_x$
恒等关系：$I_x$

关系的相等

定义域与值域：$dom(R)$和$ran(R)$

关系图，关系矩阵

关系及其性质

自反，反自反，对称，反对称，传递

关系的运算

作为集合时的运算，逆运算，复合运算，闭包运算

集合运算

交集，并集，差集，补集，对称差

R, S	$R \cap S$	$R \cup S$	$R - S$	$R \oplus S$	$\sim R$
自反	$\surd$	$\surd$
反自反	$\surd$	$\surd$	$\surd$	$\surd$
对称	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
反对称	$\surd$		$\surd$
传递	$\surd$

逆运算

$dom(R^{-1})=ran(R)$
$ran(R^{-1})=dom(R)$

定理：若 $R, R_i \, (i=0, 1, 2, \dots)$ 都是从集合 $A$ 到集合 $B$ 的二元关系，$K$ 为 $N$ 的非空子集，则有

(1) $(R^{-1})^{-1} = R$;
(2) $({\sim}R)^{-1} = {\sim}(R^{-1})$;
(3) 如果 $R_1 \subseteq R_2$, 则 $R_1^{-1} \subseteq R_2^{-1}$;
(4) 如果 $R_1 = R_2$, 则 $R_1^{-1} = R_2^{-1}$;
(5) $(\bigcup_{n \in K} R_n)^{-1} = \bigcup_{n \in K} (R_n^{-1})$;
(6) $(\bigcap_{n \in K} R_n)^{-1} = \bigcap_{n \in K} (R_n^{-1})$;
(7) $(R_1 - R_2)^{-1} = R_1^{-1} - R_2^{-1}$;
(8) $(R_1 \oplus R_2)^{-1} = R_1^{-1} \oplus R_2^{-1}$.

逆运算保持五个关系

R	自反	反自反	对称	反对称	传递
$R^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$

定理：$R$是自反的（反自反，对称，反对称，传递）当且仅当$R^{-1}$是自反的（反自反，对称，反对称，传递）

定理：集合$A$上的二元关系$R$是对称的当且仅当$R=R^{-1}$.

复合（合成）运算

定理：设$A,B,C,D$为任意四个集合，二元关系$R_1 \subseteq A \times B, \quad R_2, R_3 \subseteq B \times C, \quad R_4 \subseteq C \times D :$

1. 若 $R_2 \subseteq R_3$, 则 $R_1 \circ R_2 \subseteq R_1 \circ R_3$ 且 $R_2 \circ R_4 \subseteq R_3 \circ R_4$;
2. $R_1 \circ (R_2 \cup R_3) = (R_1 \circ R_2) \cup (R_1 \circ R_3)$;
3. $(R_2 \cup R_3) \circ R_4 = (R_2 \circ R_4) \cup (R_3 \circ R_4)$;
4. $R_1 \circ (R_2 \cap R_3) \subseteq (R_1 \circ R_2) \cap (R_1 \circ R_3)$;
5. $(R_2 \cap R_3) \circ R_4 \subseteq (R_2 \circ R_4) \cap (R_3 \circ R_4)$;
6. $(R_1 \circ R_2)^{-1} = R_2^{-1} \circ R_1^{-1}$;
7. $(R_1 \circ R_2) \circ R_4 = R_1 \circ (R_2 \circ R_4)$.

关系的幂次

$R^0=I_A$

定理：

(1) $(R^n)^{-1}=(R^{-1})^n$;
(2) $R^n\circ R^m=R^{n+m}$;
(3) $(R^n)^{m}=(R^{nm})$.

定理：设有限集$A$恰有$n$个元素。若$R$为$A$上的二元关系，则有$s,t\in N,$使$s\lt t\leq 2^{n^2}$且$R^s=R^t$

$R, S$	自反	反自反	对称	反对称	传递
$R \circ S$	$\surd$	$\times$	$\times$	$\times$	$\times$

定理：
(1)$R$为自反的当且仅当$I_A\subseteq R$
(2)$R$为反自反的当且仅当$I_A\cap R=\varnothing$
(3)$R$为对称的当且仅当$R\not=R$
(4)$R$为反对称的当且仅当$R\cap R^{-1}\subseteq I_A$
(5)$R$为传递的当且仅当$R\circ R\subseteq R$

关系合成的矩阵表示：矩阵相乘

闭包运算

$R$的自反（对称，传递）闭包即为包含$R$的最小自反（对称，传递）关系：
(1)$R'$是自反的（对称的，传递的）
(2)$R\subseteq R'$
(3)对于$A$上的任何自反（对称，传递）关系$R''$,如果$R\subseteq R''$,则$R'\subseteq R''$
自反$r(R)$，对称$s(R)$，传递$t(R)$.

定理：
(1)$R$是自反的当且仅当$r(R)=R$
(2)$R$是对称的当且仅当$s(R)=R$
(3)$R$是传递的当且仅当$t(R)=R$

定理：
(1)$r(R) = R \cup I_A$;
(2)$s(R) = R \cup R^{-1}$;
(3)$t(R) = \bigcup_{n=1}^{\infty} R^n$.

定理：设$R$是集合$A$上的关系，$A$有$n$个元素，则$t(R)=\bigcup_{i=1}^n R^i$

定理:设二元关系$R_1,R_2$是集合$A$上的二元关系，且$R_1\subseteq R_2$,则
(1)$r(R_1)\subseteq r(R_2)$
(2)$s(R_1)\subseteq s(R_2)$
(3)$t(R_1)\subseteq t(R_2)$

$R$	$r(R)$	$s(R)$	$t(R)$
自反性	$\surd$	$\surd$	$\surd$
对称性	$\surd$	$\surd$	$\surd$
传递性	$\surd$	$\times$	$\surd$

定理：
(1)$rs(R)=sr(R)$;
(2)$rt(R)=tr(R)$;
(3)$st(R)\subseteq ts(R)$;

次序关系

$<A,\leq>$

偏序关系，严格偏序关系，全序关系，良序关系

偏序关系：自反，反对称，传递
严格偏序关系（拟序关系）：反自反，传递$\rightarrow$反对称
全序关系：偏序且任意$x,y\in A$是可比的

哈斯图

覆盖：最小的更大元素

最大元，最小元，极大元，极小元

良序关系：偏序$<A,\leq>$且$A$的每一个非空子集都有一个最小元

定理：良序关系的充要条件：
(1)$\leq$为$A$上的全序关系，且每个非空子集都有极小元
(2)不存在$A$中元素的无穷递降序列

定理：偏序（全序）关系的逆关系仍是偏序（全序）关系，良序关系的逆关系未必是良序关系

等价关系与划分

相容关系；自反，对称

定理：$R$为$A$上的相容关系当且仅当$r(R)=s(R)=R$

等价关系：自反，对称，传递

定理：$R$为$A$上的等价关系当且仅当$r(R)=s(R)=t(R)=R$

定理：若$R$为集合$A$上的二元关系，则$tsr(R),trs(R),rts(R)$都是$A$上的等价关系

定理：若$R$为非空有限集$A$上的二元关系，则$R$为$A$上的等价关系的充要条件为R有简化关系图，且其每个分支都是完全图

等价类与商集与秩：对于每个$x∈A$，$A$中与$x$有关系R的元素的集合称为$x$关于$R$的等价类简称为$x$的等价类，记作$[x]_R$.设$R$为集合$A$上的等价关系。称集合 $\{ [x]_R \mid x \in A \}$为$A$关于$R$的商集，并记为$A/R$，并称$n(A/R)$为$R$的秩。

定理：设$R$是非空集合$A$上的等价关系，则有:

(1) 对于每个 $x \in A, \, x \in [x]_R$, 即 $[x]_R$ 是 $A$ 的非空子集.
(2) $[x]_R = [y]_R$ 当且仅当 $xRy$.
(3) 若 $x, y \in A$ 且 $x \bar{R} y$, 则 $[x]_R \cap [y]_R = \varnothing$.
(4) $\bigcup_{x \in A} [x]_R = A$.

划分：本质是一个集类$\Pi \subseteq \mathcal{P}(A)$
(1)若$S\in\Pi$,则$S\not=\varnothing$
(2)$\cup\Pi=A$
(3)若$S_1,S_2\in\Pi$,且$S_1\cap S_2\not=\varnothing$,则$S_1=S_2$.

一个等价关系和一个划分互相确定

函数

部分函数，全函数

定义域，值域

(1)$domf=X$,$X$到$Y$的全函数
(2)$domf\subset X$,$X$到$Y$的严格部分函数
(3)$ranf=Y$,$X$到$Y$上的部分函数
(4)$ranf\subset Y$,$X$到$Y$内的部分函数
(5)一一对应，1-1部分函数

像与源像：$f[A]$和$f^{-1}[B]$
$ranf=f[X]$
$domf=f^{-1}[Y]$

限制与延拓：$f\cap (A\times Y)$称为$f$在$A$上的限制，记作$f|_A$，也可称$f$为$f|_A$到$X$的延拓

定理：
(1) 若 $A_1 \subseteq A_2 \subseteq X$, 则 $f[A_1] \subseteq f[A_2]$;
(2) 若 $B_1 \subseteq B_2 \subseteq Y$, 则 $f^{-1}[B_1] \subseteq f^{-1}[B_2]$;
(3) 若 $A \subseteq \text{dom } f$, 则 $A \subseteq f^{-1}[f[A]]$;
(4) 若 $B \subseteq \text{ran } f$, 则 $B = f[f^{-1}[B]]$.

定理：
(1) $f[\bigcup \mathcal{A}] = \bigcup \{ f[A] \mid A \in \mathcal{A} \}$;
(2) 若 $\mathcal{A} \neq \varnothing$, 则 $f[\bigcap \mathcal{A}] \subseteq \bigcap \{ f[A] \mid A \in \mathcal{A} \}$;
(3) $f^{-1}[\bigcup \mathcal{B}] = \bigcup \{ f^{-1}[B] \mid B \in \mathcal{B} \}$;
(4) 若 $\mathcal{B} \neq \varnothing$, 则 $f^{-1}[\bigcap \mathcal{B}] = \bigcap \{ f^{-1}[B] \mid B \in \mathcal{B} \}$.

定理：若$A$和$B$都是有限集，则$n(B^A)=(n(B))^{n(A)}$

单射，满射，双射

自然映射/正则映射：$\phi=\{<x,[x]_R>|x\in A\}$

函数的复合（合成）

$f\circ g=f(g)$

复合保持单值性

定理：$dom(g\circ f)=f^{-1}[domg]$且$ran(g\circ f)=g[ranf]$.若$f$和$g$都是全函数，则$g\circ f$也是全函数

结合律：$h\circ(g\circ f)=(h\circ g)\circ f$

函数的幂
$f^0=I_X$

定理：满射，单射，双射复合后均保留

定理：
(1)若$g\circ f$是满射，则$g$是满射
(2)若$g\circ f$是单射，则$g$是单射
(3)若$g\circ f$是双射，则$g$是满射且$f$是单射
左满右单

逆函数

$f^{-1}$
左可逆（左逆），右可逆（右逆），可逆（逆）

定理：下列说法等价：
(1)$f$为单射
(2)$f$为左可逆
(3)$f$可左消去，即对任意集合$Z$及任意的$g:Z\rightarrow X$和$h:Z\rightarrow X$当$f\circ g=f\circ h$时，皆有$g=h$
另一侧同理。

定理：设$X$和$Y$为二集合，若$f : X→Y$既是左可逆的，又是右可逆的，则$f$是可逆的，且$f$的左逆和右逆都等于$f$的唯一的逆

定理：下列说法等价：$f$双射；既左可逆又右可逆；可逆；逆关系即为逆函数

复合与逆：$(g\circ f)^{-1}=f^{-1}\circ g^{-1}$

集合的特征函数

函数的比较和运算

特征函数：
(1) $0 \leq \chi_A \leq 1$
(2) $\chi_A = 0$ 当且仅当 $A = \varnothing$
(3) $\chi_A = 1$ 当且仅当 $A = U$
(4) $\chi_A \leq \chi_B$ 当且仅当 $A \subseteq B$
(5) $\chi_A = \chi_B$ 当且仅当 $A = B$
(6) $\chi_{\sim A} = 1 - \chi_A$
(7) $\chi_{A \cap B} = \chi_A \cdot \chi_B$
(8) $\chi_{A \cup B} = \chi_A + \chi_B - \chi_A \cdot \chi_B$
(9) $\chi_{A - B} = \chi_A - \chi_A \cdot \chi_B$
(10) $\chi_A \cdot \chi_B = \chi_A$ 当且仅当 $A \subseteq B$
(11) $\chi_A \cdot \chi_A = \chi_A$ (幂等律)

基数

自然数与数学归纳法

暂略。

基数

等势：存在双射。自反，对称，传递（即等价关系）

有穷集，无穷集

定理：任何有穷集合不能与它的真子集等势

定理：任意有穷集$A$与唯一的一个自然数等势

定理：$\#(A)\leq \#(B)$和$\#(b)\leq \#(a)$至少有一个成立，即任何两个基数可以比较大小

基数相等是等价关系
基数小于等于是全序

定理：$\#(b)\leq \#(a)$当且仅当存在从$A$到$B$的满射

可数无穷集合：与自然数集合$\mathcal N$等势(基数为$\aleph_0$)

可数集合：有穷集合或可数无穷集合
不可数集合：无穷且不可数的集合

定理：以下等价：$A$为无穷集合；$A$有可数无穷子集；$A$有与它等势的真子集

定理：可数无穷集合的无穷子集必是可数无穷的

定理：$\forall A,\#A\lt\#\mathcal{P}(A)$

图论

图论的基本概念

$G=<V,E,\Psi>$

• V称为G的节点集，E称为G的边集
• 结点数目称为阶
• $\Psi$是从边集E到节点的偶对（无序或有序）集上的函数

无向图，有向图

关联，邻接：

• $e$与$v_1$互相关联
• $v_1$和$v_2$既是$e$的起点，也是终点，称两点邻接
• 两条不同边$e_1$和$e_2$与同一个结点关联，则称$e_1$和$e_2$邻接

自圈，平行边
无自圈和平行边称为简单图，否则为伪图

度：与结点关联的边数

• 对无向图，$d_G(v)$
• 对有向图，出度$d_G^+(v)$，入度$d_G^-(v)$，度$d_G(v)$

定理：握手定理，设无向图$G=<V,E,\Psi>$，有$m$条边，则$\sum_{v\in V}d_G(v)=2m$

奇结点：度为奇数的结点
偶结点：度为偶数的结点
孤立点：度为0的结点
端点：度为1的结点

定理：任何无向图中都有偶数个奇结点

零图；结点都是孤立点
平凡图：一阶零图
d度正则图：所有结点的度均为自然数$d$的无向图
完全无向图：如果$n$阶简单无向图$G$是$n-1$度正则图，记为$K_n$
完全有向图：每个结点的出度和入读均为$n-1$的$n$阶简单有向图

悬挂边，悬挂点

同构的必要条件：

• 相同的节点个数，边数，结点度数
• 双射$f$保持结点之间的邻接关系
• 双射$g$保持结点之间的邻接关系

*线图$C_n$，轮图$W_n$，立方图$Q_n$，二分图，完全二分图$K_{m,n}$

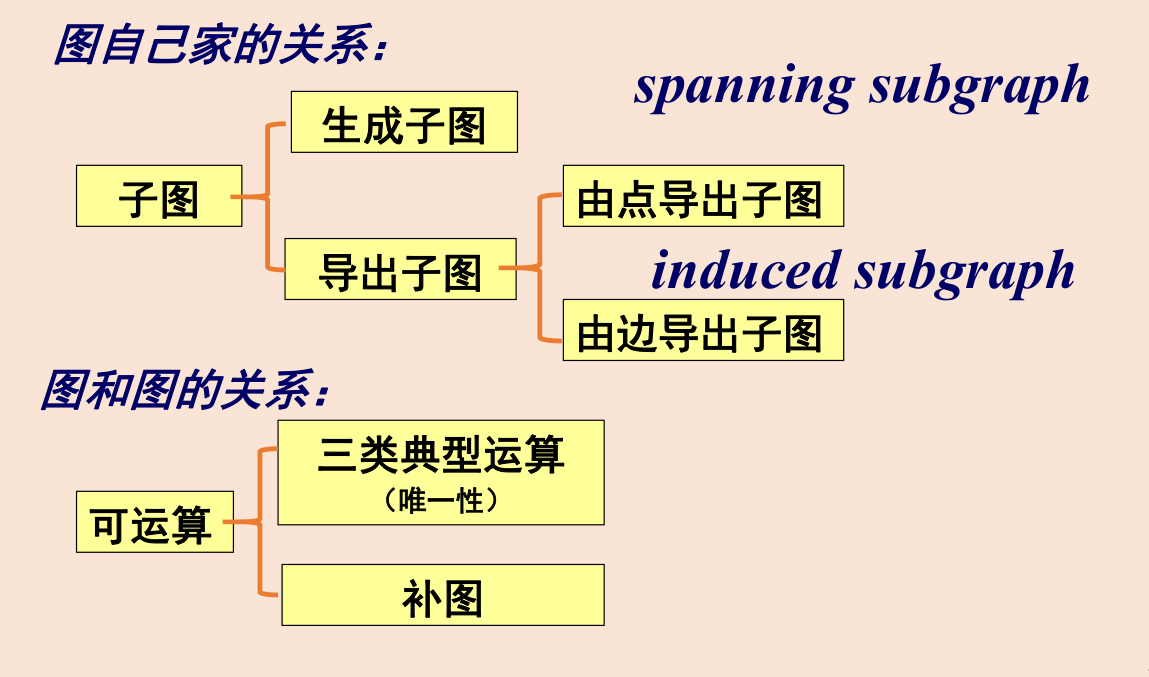
子图和图的运算

子图：$V'\subseteq V,E'\subseteq E, \Psi'\subseteq\Psi$
真子图：$V'\subseteq V,E'\subset E, \Psi'\subset\Psi$
生成子图：$V'=V,E'\subseteq E, \Psi'\subseteq\Psi$(包含所有点)

结点导出子图：

• $G[V']$:以$V'$为节点集合的最大子图
• $G-V'$:从$G$中去掉$V'$中的结点以及与这些结点关联的所有边而得到的$G$的子图

边导出子图：$G[E']$

设$G=<V,E,\Psi>$，$G'=<V',E',\Psi'>$同为无向图或有向图

• 可运算：$\forall e\in E\cap E',\Psi(e)=\Psi'(e)$
• 不相交
• 边不相交

交，并，环和

定理（图运算的唯一性）：设两图可运算，若$V_1\cap V_2\not=\varnothing$,则存在唯一的$G_1\cap G_2$.一定存在唯一的$G_1\cup G_2$和$G_1\oplus G_2$

$G-E'$：从$G$中去掉$E'$中的边所得到的$G$的子图（与$E'$中的边相关联的结点并不去掉）

$G+E'_{\Psi'}$:由$G$增加$E'$中的边所得到的图，其中$\Psi'$指出$E'$中的边与结点的关联关系

补图：$\bar G=K_n-E$

路径，回路和连通图

路径（链），可达，距离，连通性

$v_0e_1v_1e_2...v_{n-1}e_nv_n$为$v_0$至$v_n$的路径，$n$称为该路径的长度

• 如果$v_0=v_n$，则称该路径为闭的，否则称为开的
• 如果$e_1,e_2,...,e_n$互不相同，则称该路径为简单的（迹）
• 如果$v_0,v_1,...,v_n$互不相同，则称该路径为基本的（路）

定理：如果存在从$v$到$v'$的路径，则存在从$v$到$v'$的基本路径

定理：$n$阶图中的基本路径长度小于$n$

可达：存在路径
距离：若两点可达，则路径中长度最短者为测地线，并称该测地线的长度为两点的距离，记作$d(v_1,v_2)$。若不可达，则$d(v_1,v_2)=\infin$

直径：图$G=<V,E,\Psi>$的直径为$max_{v,v'\in V}d(v,v')$

加权图：

• 路径中所有边的加权长度之和称为该路径的加权长度
• 两点加权长度最小的路径称为加权路径，长度称为加权距离

迪杰斯特拉算法(Dijkstra)

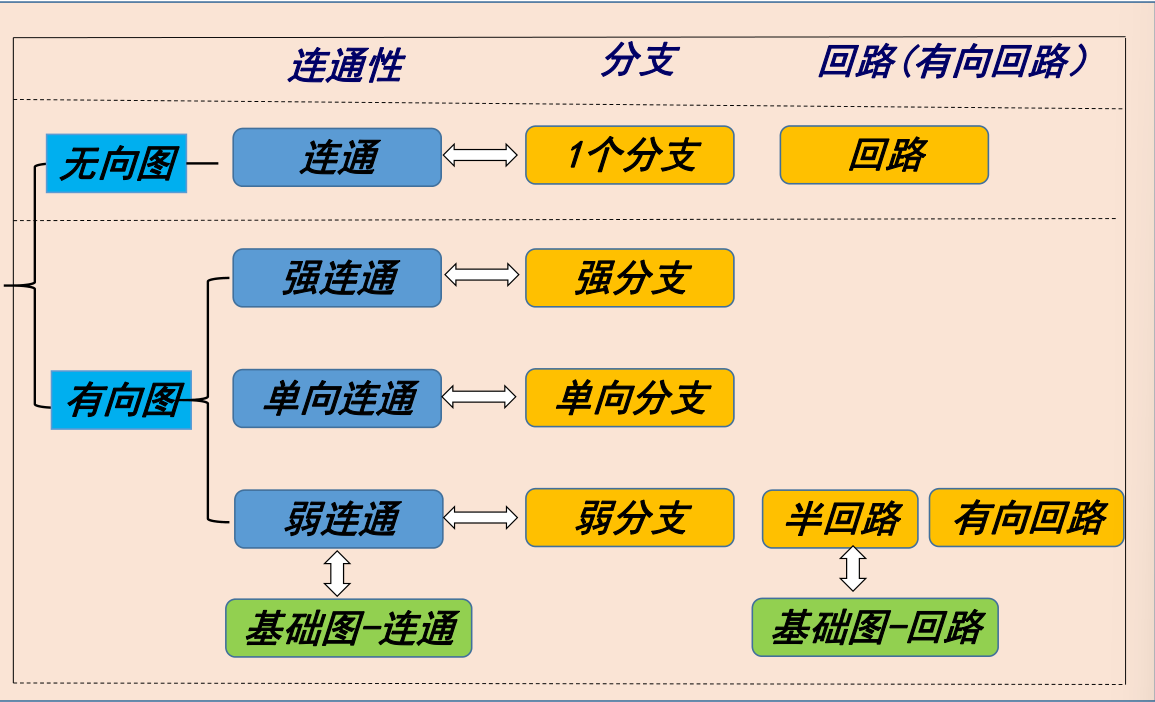
连通性：连通图，非连通图

有向图→有向图的基础图

• 强连通：任意两个结点互相可达
• 单向连通：对任意两个结点，必有一个结点可达另一个
• 弱连通：基础图是连通的

分支：无向图G的极大连通子图称为G的分支

• 强分图：最大的强连通子图（强分支）
• 单向分图：最大的单向连通子图（单向分支）
• 弱分图：最大的弱连通子图（弱分支）

定理：连通无向图恰有一个分支；非连通无向图的分支多于一个

半路径：有向图的基础图的路径，称为该有向图的半路径。分为正向边和反向边

回路：连通2度正则图
半回路：基础图是回路的有向图
有向回路：每个结点的出度和入读均为1的弱连通有向图

定理：设$v$是图$G$任意节点，$G$是回路（或有向回路），当且仅当：$G$的阶与边数相等，且在$G$中存在一条$v$到$v$的闭路径，使得除了$v$在该闭路径中出现两次外，其余结点和每条边都在该闭路中恰出现一次

如果回路（有向回路，半回路）$C$是图$G$的子图，则称$G$有回路（有向回路，半回路）
非循环图：没有回路的无向图和没有半回路的有向图称为

定理：如果有向图$G$有子图$G'$，使得对于$G'$的任意结点$v$，皆有$d_{G'}^+(v)>0$（或$d_{G'}^-(v)>0$），则$G$有有向回路

W-过程：从$G$中去掉$v$（出度或入度为0的边）和与之关联的边的过程
若$n$阶有向图$G$没有有向回路，则经过$n-1$次W-过程得到平凡图

定理：图$G$不是非循环图当且仅当$G$有子图$G'$，使得对于$G'$的任意结点$v$，皆有$d_{G'}(v)>1$（或对任意子图存在结点$v$，使$d_{G'}(v)\leq1$）

欧拉图和哈密顿图

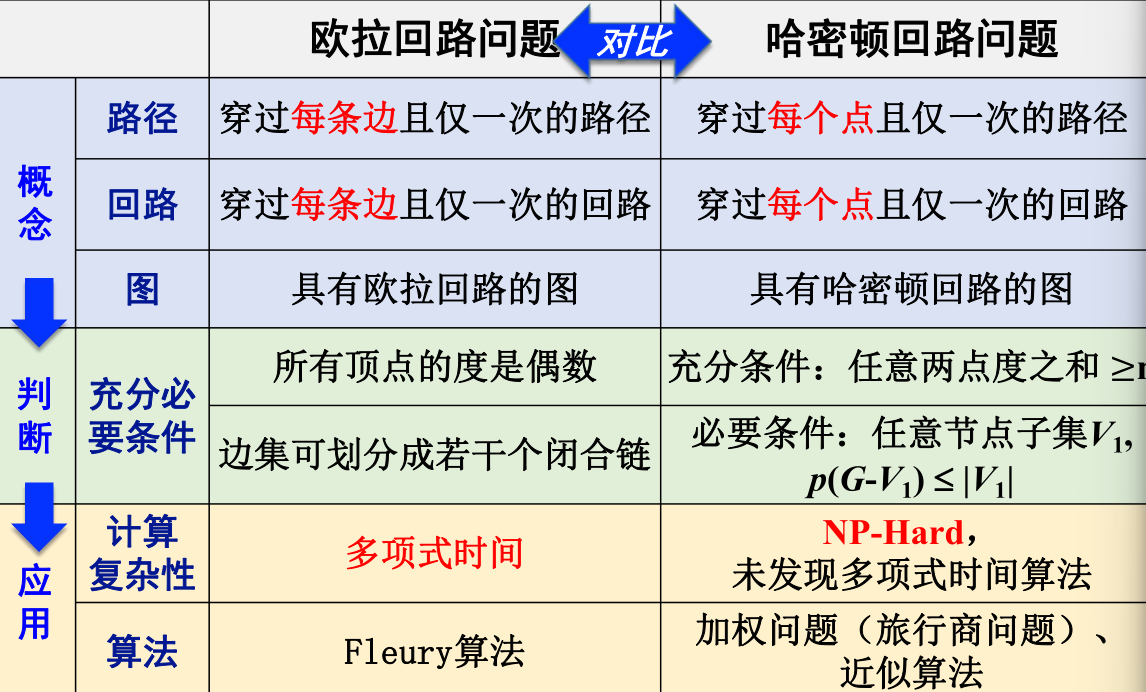
欧拉图

• 每个结点都是偶节点的无向图称为欧拉图
• 每个结点的出度和入度都相等的有向图称为欧拉有向图

定理：$G$是连通无向图，其是欧拉图当且仅当它有欧拉回路

定理：设$G$为连通无向图，$v_1,v_2\in V$且$v_1\not=v_2$。则$G$有一条两点的欧拉路径当且仅当$G$恰有两个奇结点$v_1,v_2$

定理：设$G$为弱连通的有向图，$G$是欧拉有向图当且仅当$G$有欧拉闭路

定理：$G$为弱连通的有向图。$G$有一条从$v_1$到$v_2$的欧拉路径当且仅当$d_G^+(v_1)=d_G^-(v_1)+1,d_G^+(v_2)=d_G^-(v_2)-1$且对$G$的其他节点，均有$d_G^+(v)=d_G^-(v)$

定理：如果$G_1,G_2$是可运算欧拉图，则$G_1\oplus G_2$是欧拉图

*Fleury算法

哈密顿图

• 如果回路（有向回路）$C$是图$G$的生成子图，则称$C$是$G$的哈密顿回路（哈密顿有向回路）
• 图$G$中包含它的所有结点的基本路径称为$G$的哈密顿路径
• 有哈密顿回路（哈密顿有向回路）的图称为哈密顿图（哈密顿有向图）

必要条件：

• 标点法：黑白两种颜色着色，使相邻点颜色不同
• 去边法：去掉每个点两条以上的边

定理：设$G$是哈密顿图，则对$V$的任意非空真子集$V_1$有$W(G-V_1)<=|V_1|$

充分条件：

• 哈密顿图一定不存在悬挂边
• 哈密顿图中不存在孤立顶点
• $n\geq 2$时，$K_n$是哈密顿图

定理：
(1)$G$是$n(n\geq 2)$阶简单图，如果$G$中任意一对顶点$u$和$v$，都满足$d_G(u)+d_G(v)\geq n-1$，则$G$中存在哈密顿道路
(2)$G$是$n(n\geq 3)$阶简单图，如果$G$中任意一对顶点$u$和$v$，都满足$d_G(u)+d_G(v)\geq n$，则$G$中存在哈密顿道路

推论：
(1)$G$是$n(n\geq 3)$阶简单图，如果$G$中任意顶点的度数至少是$\frac{n}{2}$，则$G$是哈密顿图
(2)$G$是一个$(n,m)$简单图，若$m\geq\frac{(n^2-3n+6)}{2}$，则$G$是哈密顿图

图的矩阵表示

邻接矩阵

• 对矩阵$X$,$x_{ij}^{(m)}$表示$X^m$的第$i$行第$j$列元素
• 在$X(G)$中，若$x_{ij}=r$，则说明从$v_i$到$v_j$中存在$r$条长度为$1$的路径

定理：$n$阶图$G$，若$X$是$G$的邻接矩阵且$i\leq i,j\leq n$，则$x_ij^{(m)}$等于$G$中从$v_i$到$v_j$的长度为$m$的路径数

可达矩阵（路径矩阵）

距离矩阵

关联矩阵：

• 点为列，边为行
• 对有向图，起点为$1$，终点为$-1$

定理：设$X$和$P$分别是$n$阶简单图$G$的邻接矩阵和路径矩阵，记$X^{(0)=I_n}$，则$P=\sum_{k=0}^{n-1}X^{(k)}$

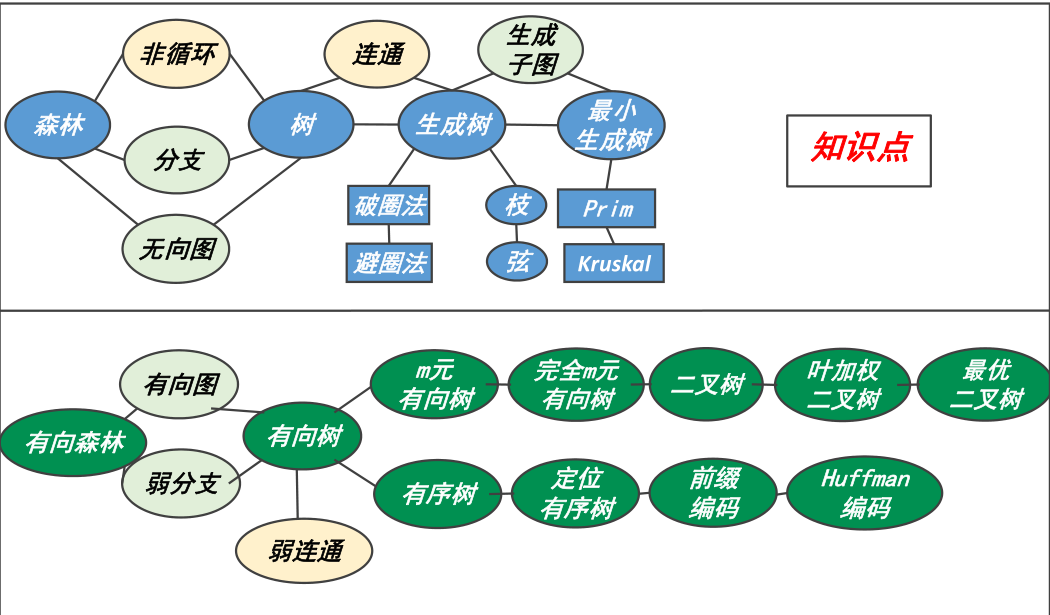
树，有向树和有序树

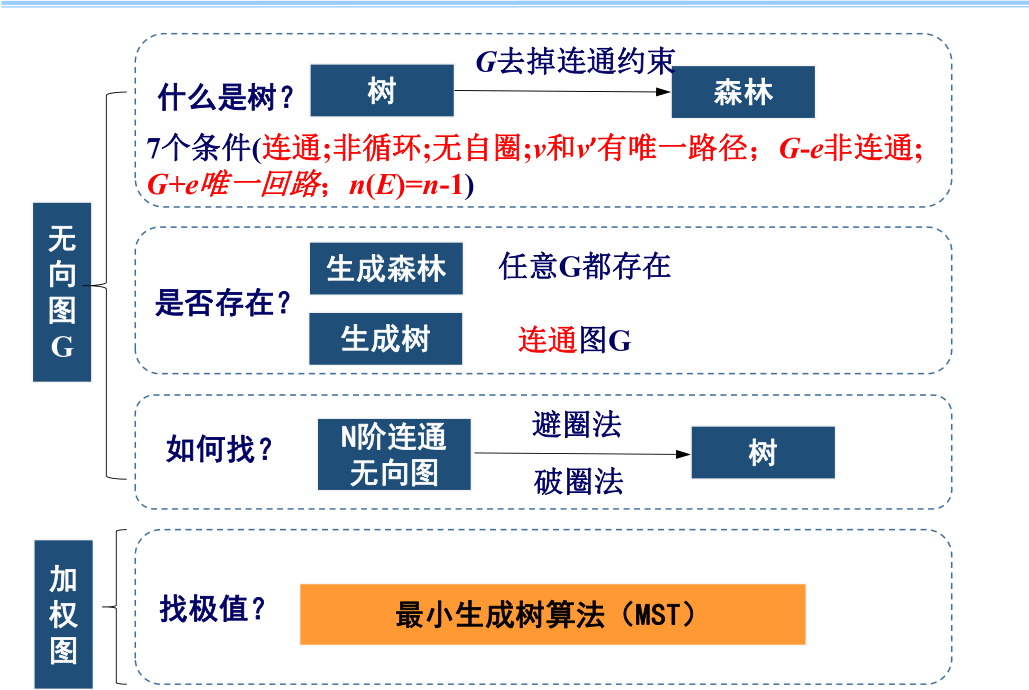
树：非循环的连通无向图

森林：每个分支都是树的无向图

定理：如果森林$F$有$n$个结点，$m$条边$k$个分支，则$m=n-k$

生成树，生成森林

定理：设无向图$G$连通，则$G$至少有一个生成树

最小生成树：Prim算法和Kruskal算法

设$T$为连通无向图$G$的生成树，称$T$的边为枝，$G$不属于$T$的边为弦

定理：设$G$是有$m$条边的$n$阶连通无向图，则对于$G$的任何生成树$T$，都有$n-1$个枝和$m-n+1$个弦

若$n$阶无向图$G$有$m$条边和$k$个分支，则$G$的余圈秩$r=n-k$，圈秩$μ=m-n+k$

基本回路：设$T$是连通无向图$G$的生成树，$G$的只包含一条弦的回路称为基本回路

定理：设$T$是连通无向图$G$的任意生成树
(1)基本回路的数目等于$G$的圈秩$μ$
(2)对于$G$的任意回路$C$，总可以找到若干个基本回路，使$C$与$C_1\oplus C_2\oplus...\oplus C_k$的差别仅在于孤立点

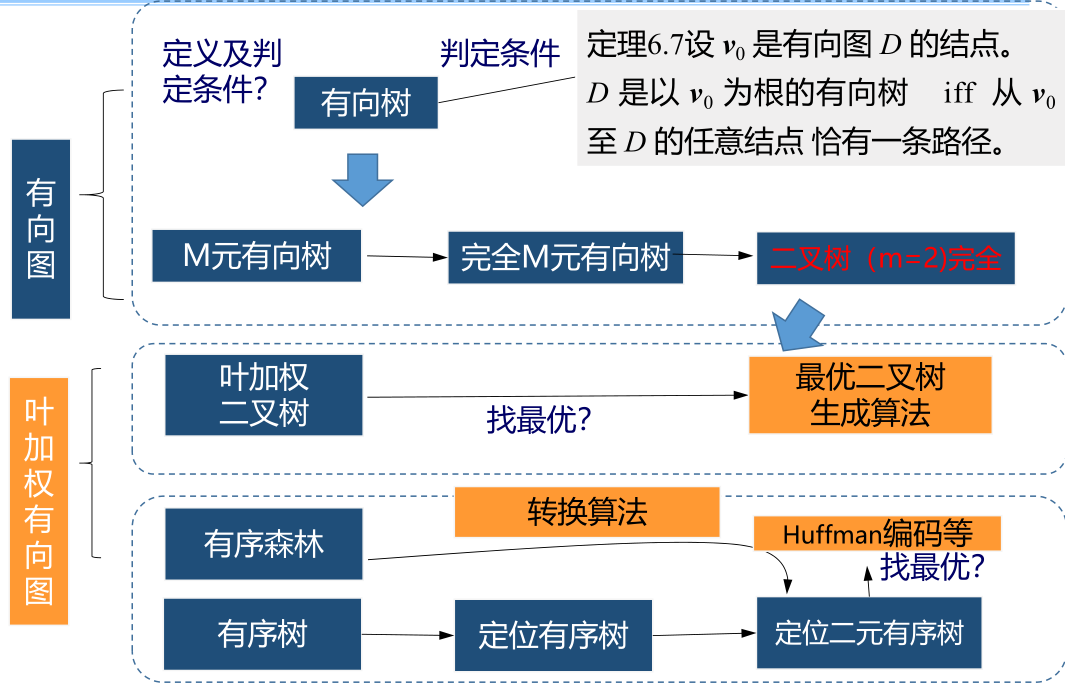
有向树：根，叶，分支节点，级，高度

定理：设$v_0$是有向图$D$的结点。$D$是以$v_0$为根的有向树当且仅当从$v_0$到$D$的任意结点恰有一条路径

有向森林：每个若分支都是有向树的有向图

m元有向树，完全m元有向树

叶加权二叉树，最优二叉树

有序树，有序森林，定位有序树

有序森林和定位二元有序树的一一对应